摘要:以计算流体力学为工具, 详细分析计算了流体流过孔板的层流流场分布以及压力降。 计算了 β=d D =0 .5时的流出系数, 并根据计算结果拟合出流出系数与 Re 的关系式。 在以往孔板的层流流场模拟中, 雷诺数不超过 150, 而作者所编的计算程序能够计算雷诺数从 0 ~ 500 之间所有孔板流场, 从而为实际应用奠定了良好的基础。
1、引言:
孔板被广泛地应用在天然气、化工装置的流量测量等场所,其优点是几何形状简单、耐用、数据可靠。在孔板计量中 ,流出系数是孔板计量准确程度的主要参数。而随着计算机技术和流体力学的发展,人们可以通过数值模拟来获得流出系数。通过孔板流场的数值模拟, 能够获得流体流经孔板的全部信息。在实际过程中, 例如向压缩机添加冲洗油、冷却水、各种阻聚剂等 , 其流量都比较小, 属于低流量范围,即层流 ,且都用孔板控制流量。如何根据孔板压力差计算出流量, 就成为现场流量控制和调查

事故原因的主要依据 , 也为优化控制提供数据和理论基础。而实际工作中 ,缺乏流出系数和相关参数。本文正是在这一背景下 , 进行低雷诺数的孔板流场数值模拟 ,即层流模拟。模拟程序对实际应用有着重要的意义。
2、数学模型:
根据孔板的几何形状及参数 , 将管路及孔板简化为如图1 所示的几何形状。
2.1、基本方程:
根据图 1 几何形状 ,流场计算将在轴对称、圆柱坐标系下进行。假设流体为不可压缩、等温。不可
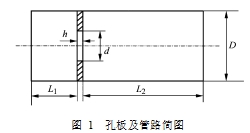
图 1 孔板及管路简图
压缩二维轴对称稳态流动的基本方程如下:

压缩二维轴对称稳态流动的基本方程
2.2、不可压缩流体轴对称流动方程的无量纲化:
假设:X =
Dx , R =
Dr , P =
ρup2 , U =
uum , V =
uvm ,mRe =ρum D μ,其中 um 为入口平均速度。将上述参

数代入式(1)、(2)、(3),并简化得:
2.3 、定解条件 :
考虑到区域的对称性, 故取实际区域的一半作为计算区域。边界条件包括进口、出口、轴对称边界及壁面四部分。
(1)进口边界
假设进口速度分布为抛物线分布, 即:
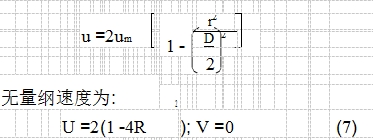
(2)出口边界
假设计算出口边界条件为充分发展流动 ,即:
U X =0 ; V =0
|
(3)轴对称边界 |
|
|
|
|
|
|
|
|
|
|
|
R =0 : U R =0 ; V =0 |
(9) |
|
(4)壁面条件 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
,R =0.5 ,0 ≤X ≤X 1 : |
|
|
a当 X1 =D |
|
|
|
U =0 , |
V =0 |
|
|
|
|
(10) |
|
b当 X1 =L1 |
, |
1 |
|
d |
<R < |
1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
2 D |
2 |
|
|
|
|
|
|
|
|
U =0 , |
V =0 |
|
|
|
|
(11) |
|
L1 |
+h |
|
|
|
|
|
|
1 d |
|
|
c当 X2 = D |
, X1 |
<X <X 2 , R |
= |
|
|
|
: |
|
2 |
D |
|
|
U =0 , |
V =0 |
|
|
|
|
(12) |
|
d当 X3 =L1 |
+h +L |
2 , X2 ≤X ≤X3 , R =0.5 : |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
U =0 , |
V =0 |
|
|
|
|
(13) |
2.4、模型的求解:
本文采用区域扩充法 ,将整个计算区域扩充为如图2 所示。
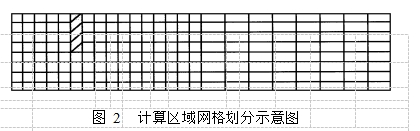
阴影部分为扩充区域 , 即孔板位置。在扩充区域 ,设粘度系数为无穷大。将整个计算区域划分为20 ×353 个非均分网格 。取 L1 =3D , L2 =40D , h =3 D 。采用交错网格的控制容积法进行求解 。通过乘方格示对上述基本方程和边界条件离散化 ,编程上机计算。程序中流场求解采用 SIMPLE 算法。方程组求解采用块修正及双向 TDMA 线迭代技术。
|
3 |
计算结果 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1 |
流出系数 |
|
|
|
|
|
|
|
|
|
|
不可压缩流体流经孔板的流量公式为 : |
|
|
|
|
|
|
|
|
(πd2 4) 2 |
|
|
|
|
|
|
|
Q =Cd |
|
|
ρ(p′1 -p′2) (14) |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
1 |
-(d D) |
|
|
|
|
|
上式中, Q 为不可压缩流体流经孔板的流量 , ρ为密 |
|
|
|
|
|
度 , Cd 为流出系数 , p′1-p′2 为流经孔板的压力差。 |
|
|
|
将 Q =πD2 um 4 和 p′1-p′=(2P1 -P2 )ρum2 代入上 |
|
式得: |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
D |
2 |
|
|
4 |
|
1 |
|
|
|
Cd = |
|
|
|
|
1 -(d D) |
|
|
(15) |
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
2 |
|
d |
|
|
|
|
|
-P2 |
|
式中 ,P 1 、P2 为无量纲压力。根据无量纲压力差 ,由 |
|
上式即可计算出流出系数。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2 数值模拟计算结果与实验值的比较 |
|
|
|
|
(1)数值模拟结果的验证 |
|
|
|
|
|
利用所编制的计算机程序分别计算了文献[ 1] |
|
所给出的 Re 工况。计算结果与文献[ 1] 的实验值 |
|
比较见表 1 : |
|
|
|
|
|
|
|
表 1 流出系数 Cd 与 Re 对应表 |
|
|
|
|
|
|
|
|
|
|
|
|
Re |
2.5 |
5.0 |
10.0 |
25 .0 |
|
|
|
|
|
|
|
|
|
|
|
C d 计算值 |
0.354 3 |
0 .474 9 |
0.586 5 |
0.668 1 |
|
|
|
|
0.341 5 |
0 .462 9 |
0.581 9 |
0.690 0 |
|
|
|
C d 实验值 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
由数值模拟的结果与实验结果对比可知:本文 |
|
的数据模拟方法及数据是有效和可靠的。 |
|
|
(2)低雷诺数的流场分布及压力分布
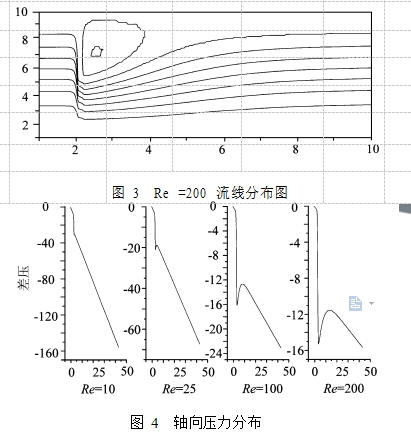
图 3 Re =200 流线分布图 图 4 轴向压力分布
3.3、流出系数的计算结果与 Re 的关系式:
流出系数一般是雷诺数、直径比和孔板几何尺寸的函数。本文模拟计算雷诺数在 2 .5~ 500 范围内的流出系数, 计算结果见表 2 :
|
|
|
|
表 2 Cd |
与 Re 关系 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
2.5 |
|
5 |
|
10 |
|
25 |
|
60 |
|
Cd |
0 .354 |
3 |
0.474 |
9 |
0.586 |
5 |
0.668 |
1 |
0.703 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Re |
100 |
|
200 |
|
300 |
|
400 |
|
500 |
|
Cd |
0 .716 |
7 |
0.727 |
4 |
0.734 |
9 |
0.738 |
0 |
0.739 5 |
|
|
|
|
|
|
|
|
|
|
|
根据上述数据, 采用***小二乘法, 拟合出 :β =d D =0 .5时, Cd 与 Re 的关系如图 5 。拟合关系式为:
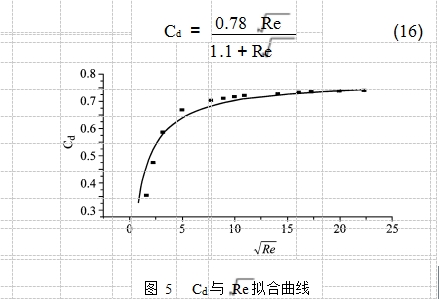
图 5 Cd 与 Re拟合曲线
|
3.4 |
应用举例 |
|
|
|
|
|
|
|
|
|
|
1 000 kg m3 |
|
|
|
已知 d D 0 |
5 |
|
|
1 007 |
|
|
: = ., ρ= |
, μ= . × |
|
10-3 Pa s |
D |
50 mm |
|
现场测量孔板前后压差为 |
|
|
· , |
|
= |
, |
|
|
|
|
|
0.06 kPa ,计算流量 。 |
|
|
|
|
|
|
根据式(16)、(15), 假设量 Q =0 .03 m3 h , |
|
计算出平均流速 um ,求出 Re , 代入式(16), 计算出 |
|
流出系数。将流出系数代入式(14), 计算出一新流 |
|
量 Q1 。再将新流量与假设流量比较, 若 Q1 -Q ≤ |
|
10-3 ,则 Q1 为所求流量 ;否则, 以 Q1 |
为基准, 重新 |
|
假设流量,重复上述过程,直到满足要求为止。本例 |
|
***终计算结果为:Q1 =0 .028 4 m3 h 。 |
|
4、结论:
本文解决了低雷诺数孔板流量计计量工作中的实际问题。虽然 Re 在 25 ~ 500 之间的流出系数需经试验进一步确认, 但数值模拟为孔板流量计流出系数的确定提供了强有力的工具。

 导
导






