V 锥和双锥是 2 种新型差压式节流件结构。 它们具有耐磨损、抗扰动能力强、流出系数稳定、压力损失小等优点, 适用于带污物的液体和气体的测量。V 锥的加工工艺较复杂,且由于结构的不对称性使得长时间使用后或在高压下,悬臂梁会出现形变现象[6]。 针对这种局限性设计了双锥流量计,双锥结构具有对称性,提高了长期使用的稳定性,减小了管道流体压损,具有良好的流量测量特性[7]。本文以双锥流量计样机为研究对象,介绍了差压式流量计流量测量原理和实验平台,分析了所研制样机的相对示值误差、重复性、线性度和不确定度等流量计测量性能。
1、双锥流量计工作原理:
双锥流量计的一次仪表由取压管道、取压单元及节流件共同构成,如图 1(a)所示。 双锥节流件由前后 2 个成一定角度的锥体,以及将 2 个锥体相连接的圆柱体组成,如图 1(b)所示。 同标准孔板及标准喷嘴压损情况对比,双锥节流件后锥角的导流作用可减少漩涡产生的流体流动分离,从而减小了流体压损及对直管段的要求[8]。
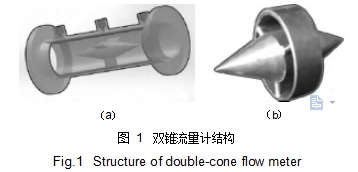
图 1 双锥流量计结构
双锥流量计工作原理同传统差压式流量计工作原理一样,在节流件处流通面积减小,流体局部收缩,流速增加,静压力减小,取压点的静压力差与流量成函数关系。 两者间关系为
|
|
|
|
|
|
|
QV =CεA0 姨2 P / ρ /姨1- βD4 |
(1) |
式中:Q
V 为体积流量(m
3/h);C 为流出系数( 无量纲); ρ 为流体密度(kg/m
3);ε 为被测介质的可膨胀系数(无量纲),对于不可压缩流体 ε=1; P 为压差(Pa),取压口在双锥节流件喉部前后的 1.5 D 处; β
D 为等效直径比, β
D2=A
0 /A, β
D 为βD =姨A0 / A =姨1-(d / D) -12nl / (πD )
式中:A0 为管道***小流通(m2),A0 =πD2 /4-πd2/4-3nl;D 为管道内径(m);d 为节流锥体喉部直径(m);n 为叶片型固定架厚度(m);l 为叶片型固定架长度(m);A 为管道横截面积(m2),A=πD2 /4。
双锥流量计样机中使用的双锥节流件前后锥角角度都为 45°,等效直径比 βD 为 0.587,D=50 mm,d=40 mm,n=2 mm,l=5 mm,喉部圆柱长 20 mm。 工况条件:介质为水(流体密度为 996 kg/m3),温度 25 ℃~28 ℃,湿度 70%~80%,大气压 101.4 kPa。
双锥节流件前差压的采样通过以 MSP430 为智能控制器制作的数据采集系统完成,样机采集系统具备多路模拟量采样及记录功能, 如图 2 所示,其中电源模块为整个样机系统供电。
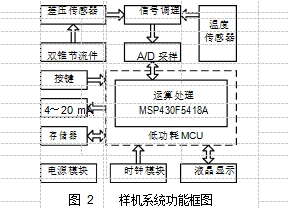
2、实验平台及流出系数确定:
由于双锥节流件尚属非标准节流件,使用前需要以水为介质对其进行实流标定。 水流量检测标准实验室使用 DN50 的实验管路, 整个水路实验设备平台由蓄水槽、变频水泵、液体稳压罐、标准水表、实验管道组成,如图 3 所示。
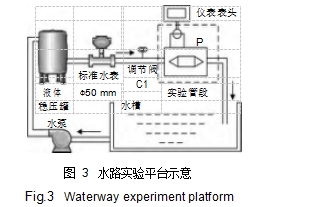
图 3 水路实验平台示意
实验按照《标准表法流量标准装置》的计量测试规程进行, 采用 0.2 级 Krohne IFM4080F 型电磁流量计作为标准表对所研制的双锥流量计样机进行累积流量标定。 由于在较大流量测量时,双锥前端所取的差压值较高, 故使用的电容式差压变送器 CECC-640 测量量程为 0~100 kPa,其测量度为 0.2
级。 在较小流量测量时,为减小满度误差带来测量影响,使用量程为 0~25 kPa 的 0.5 级变送器进行标定及测试。 输出均为标准 4~20 mA 电流信号。
在实流标定前需对标准水流量装置实验管段进行漏水检查及一次仪表安装工作,双锥节流件按其取压口倾斜向下 45°方位安装于实验管段内,利用导压管将双锥流量计节流件上游和喉部处的取压口与差压传感器相连,如图 4(a)所示,图中箭头表示流向。 为保证样机两侧流体为稳定的充分发展流, 实验平台上下游直管段分别为 100 D,20 D,满足测试要求,图 4(b)为标准水流量实验室。

表对比法 确定装置流出系数。 实验要求在 0.5~4.0 m/s的流速测量范围进行标定和测试。 测量范围内选择 8 个流量标定点, 对电磁流量 计与样机的累积流量值进行定时记录, 通过对比分析及计算得到
流出系数, 如图 5所示。
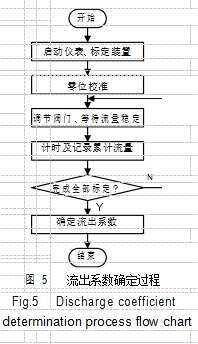
图 5 流出系数确定过程
3 、测试及数据分析 :
样机实流测试实验包括累积流量相对示值误差分析、测量重复性分析及线性度分析。测试采用容积法对多个流速点进行累积流量测量,确定的 8 个测试流速点分别是:0.5 m/s,1.0 m/s,1.5 m/s,2.0 m/s,2.5 m/s,3.0 m/s,3.5 m/s,4.0 m/s。累积容积值设置要求:0.5 m/s,1.0 m/s 流量点累积 0.5 m3;1.5 m/s,2.0 m/s 流量点累积 1 m3;2.5 m/s,3.0 m/s,3.5 m/s,4.0 m/s 流量点累积 2 m3。 标定实验要求对各流速点进行往复 5 次的重复测试实验,测量数据如表 1 所示。
|
|
|
表 1 |
累积流量实验数据 |
|
|
|
|
Tab.1 |
Test result of accumulative flow |
|
|
|
|
|
|
|
|
|
[%] |
测试点/ |
标准表 |
样机 |
相对 |
误差 重复性/ |
|
|
(m·s-1) |
读数/(m3) 读数/(m3) 误差/% |
均值/% |
% |
|
|
|
2.005 |
2.001 |
-0.20 |
|
|
|
|
|
2.019 |
2.011 |
-0.40 |
|
|
|
100 |
4.0 |
2.027 |
2.018 |
-0.45 |
-0.42 |
0.15 |
|
|
|
1.993 |
1.981 |
-0.61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2.002 |
1.993 |
-0.45 |
|
|
|
|
|
1.991 |
1.986 |
-0.25 |
|
|
|
|
|
1.973 |
1.965 |
-0.41 |
|
|
|
87.5 |
3.5 |
2.018 |
2.016 |
-0.10 |
-0.23 |
0.16 |
|
|
|
1.987 |
1.980 |
-0.35 |
|
|
|
|
|
2.008 |
2.007 |
-0.05 |
|
|
|
|
|
2.001 |
1.995 |
-0.30 |
|
|
|
|
|
1.996 |
1.992 |
-0.20 |
|
|
|
75 |
3 |
2.080 |
2.071 |
-0.43 |
-0.31 |
0.16 |
|
|
|
|
|
|
|
|
|
|
|
2.021 |
2.011 |
-0.50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.985 |
1.983 |
-0.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.976 |
1.970 |
-0.31 |
|
|
|
|
|
2.018 |
2.011 |
-0.35 |
|
|
|
|
|
|
|
|
|
|
|
62.5 |
2.5 |
2.027 |
2.023 |
-0.20 |
-0.36 |
0.12 |
|
|
|
|
2.008 |
1.999 |
-0.45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.989 |
1.979 |
-0.51 |
|
|
|
|
|
|
1.025 |
1.021 |
-0.39 |
|
|
|
|
|
|
1.013 |
1.011 |
-0.20 |
|
|
|
|
|
|
|
|
|
|
|
|
50 |
2.0 |
1.004 |
1.005 |
0.01 |
-0.20 |
0.21 |
|
|
|
0.999 |
0.998 |
-0.10 |
|
|
|
|
|
1.017 |
1.013 |
-0.40 |
|
|
|
|
|
|
1.002 |
0.997 |
-0.50 |
|
|
|
|
|
|
1.006 |
1.004 |
-0.20 |
|
|
|
37.5 |
1.5 |
1.004 |
0.999 |
-0.50 |
-0.38 |
0.22 |
|
|
|
|
1.007 |
1.006 |
0.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.999 |
0.993 |
-0.60 |
|
|
|
|
|
|
0.504 |
0.502 |
-0.40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.505 |
0.503 |
-0.40 |
|
|
|
25 |
1.0 |
0.501 |
0.496 |
-1.00 |
-0.52 |
0.27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.505 |
0.503 |
-0.40 |
|
|
|
|
|
0.499 |
0.497 |
-0.40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.503 |
0.502 |
-0.20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.504 |
0.499 |
-0.99 |
|
|
|
|
|
|
|
|
|
|
|
12.5 |
0.5 |
0.501 |
0.497 |
-0.80 |
-0.56 |
0.36 |
|
|
|
0.504 |
0.501 |
-0.60 |
|
|
|
|
|
0.503 |
0.502 |
-0.20 |
|
|
|
注:[%]表示测试点在全量程的占比率 |
|
|
各流量点累积流量单次检测的相对示值误差为
|
Eij =[Qij -(Qs)ij]/(Qs)ij ×100% |
(3) |
式中:i, j 分别表示第 i 个流量测试点和第 j 次测试;Q,Q
s 分别表示双锥流量计和标准表的累积流量值。
各流量点相对示值误差为
式中:E
i 为样机第 i 个测试点的相对示值误差;n 为该测试点测试次数,测试时 n 取 5。
重复性是一项仪表精度重要指标,它反映多次相同测量情况下,测试结果互不一致程度。 重复性误差是判断仪表随机误差大小的重要指标。 其计算公式为

|
n |
|
|
|
(Er)i =姨n-11 Σj=1 |
(Eij -Ei)2 |
(5) |

式中:(E
r)
i 表示第 i 个测试点的重复性误差。实验中取测试点中重复性误差***大值作为样机的重复性指标值。
通过上述分析计算,可得到样机各相对示值误差以及相应的重复性误差,如图 6 所示。
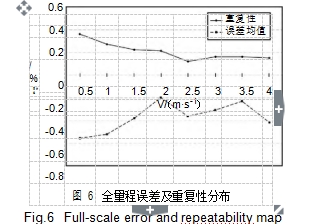
从表 1 中测量数据及图 6 可见,在 0.5 m/s,1.0 m /s 流量测试点,流量计累积流量测量误差在 0.5%以上,分别为 0.56%,0.52%;在流速 0.5 m/s 时测量重复性***差,重复性误差为 0.36%,在流速大于 0.5 m/s的流量测试点,重复性均在 0.3%以内。 且易知流量计在流量较大或较小时,其相对示值误差及测量重复性呈增大趋势。
线性度属传感器进行测量时的静态特性,在实验条件下,管道流量无法完全恒定,而且标准表与双锥流量计流过同体之间存在时间差,故宜采用时间段替代时间点的方式分析流量计的线性度。
设标准表流速即测试流速值 V
s(m/s),由式(6)可计算样机所测得的体积流量 Q
V(m
3/h)。
|
QVi, j =Qij /(Qs )ij ×Vsi ×πD2 ×900 |
(6) |
双锥流量计的输出输入 Q
V -V
s 为流量-流速关系。 根据 5 组测试数据,以及通过数学计算工具的计算得拟合直线 Q
V =KV
s +C,其中系数 K,常数 C 及线性度 γ
L 如表 2 所示。
表 2 双锥流量计线性度分析
Tab.2 Linear analysis of double-cone flowmeter

|
组号 |
系数(K) |
常数(C) |
线性度(γL) |
|
|
|
|
|
|
1 |
7.056 |
-0.01809 |
0.74 |
|
2 |
7.044 |
-0.03943 |
0.89 |
|
3 |
7.054 |
-0.01872 |
1.23 |
|
4 |
7.028 |
0.02605 |
1.33 |
|
5 |
7.052 |
-0.01481 |
1.08 |
|
|
|
|
|
由上表可知双锥流量计测量时,输出输入 Q
V -V
s的拟合直线线性度在 1.5%以内。
4、样机不确定度分析:
测量不确定度是对测量结果质量的定量表征,也是度量可信程度的重要依据。由式(1)可知,差压式流量计对体积流量测量与流出系数 C、可膨胀系数 ε、流体密度 ρ、双锥流通面积 A
0、双锥等效直径比 β
D、双锥上游与喉部压差 P 有关。节流件的加工工艺决定了 n,l,d 和 D 标准不确定度; 流出系数 C 的标准不确定度可通过式
(7)进行流量实验得到;为计算 n,l,d 和 D 的相对灵敏度值,需要引入相对灵敏度概念及相应的函数模型 y= f(x
1,x
2,…,x
n),相对灵敏度 c
ri 由式(8)表示。而可膨胀系数 ε、流体密度 ρ 和压差 P 的标准不确定度及相对灵敏度可以按照 《JJG640-94 差压式流量计测试规程》中标准孔板的 B 类不确定度评定办法得到;双锥流量计样机各分量的标准不确定度及相关灵敏度情况如表 4 所示。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C=QV姨1- βD4 /(εA0 姨2 P / ρ ) |
|
|
|
|
|
(7) |
|
|
|
|
cri =(xi / y)·( f / xi) |
|
|
|
|
|
|
|
|
(8) |
|
由式(1),式(2)和式(8)得: |
|
|
|
|
|
|
|
|
|
|
cr(d)=dB 姨- |
|
|
πd |
|
|
|
|
|
+ |
|
2dη2A0 |
|
|
|
姨 (9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2姨1- η |
4 |
|
24 3 |
|
|
|
|
|
|
|
|
|
|
D |
姨(1- η ) |
|
|
|
|
|
|
|
|
姨 |
|
|
|
|
|
|
|
|
2 |
|
|
2d2 |
24nl |
|
|
姨 |
|
|
姨 πD |
|
|
|
|
η A0 |
姨 3 |
+ |
πD |
3 |
|
|
姨 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
姨 |
|
cr(D)=DB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
|
|
姨 |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
姨 |
|
|
姨2姨1- η4 |
|
|
|
|
|
|
姨(1- η4)3 |
|
|
|
|
姨 |
|
cr(l)=lB 2 |
-3n |
|
|
|
- |
|
|
η2A0 |
|
|
|
|
· |
-12n |
2 |
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πD |
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
) |
3 |
|
|
|
|
|
|
|
|
姨1- η |
|
|
|
|
|
|
姨(1- η |
|
|
|
|
|
|
|
|
|
|
|
|
|
cr(n)=nB 2 |
-3l |
|
|
|
|
|
- |
|
|
η2A0 |
|
|
|
|
|
|
· |
-12l |
|
2 |
(12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πD2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
) |
3 |
|
|
|
|
|
|
|
|
姨1- η |
|
|
|
|
|
|
姨(1- η |
|
|
|
|
|
|
|
|
|
|
|
|
其中,B=姨1- η
4 /A
0 ;η=d / D

各分量的标准差及相对灵敏度 c
ri 确定后,相对合成标准不确定度可由式(13)求解。 在此温度对双
锥节流件各几何尺寸量的影响不予考虑。
|
|
|
|
N |
|
|
|
|
|
u |
(y)= |
2 |
2 |
(x |
|
(13) |
|
|
c ·u |
) |
|
cr |
|
|
Σ ri |
r |
i |
|
|
|
|
|
姨i=1 |
|
|
|
|
由式(13)求得双锥流量计样机的相对合成标
准不确定度为 u
cr(y)=0.00793。
除此之外, 实验分别使用了 0.2 级及 0.5 级的差压变送器, 设包含因子 k=2, 故其标准差 u (s)=
0.005/2=0.0025。
表 3 双锥流量计样机不确定度分析表
Tab.3 Double-cone flowmeter prototype
uncertainty analysis table

|
参数 不确定度来源 数值(SI) |
标准不确定度 相对灵敏度值 |
|
|
|
|
|
|
|
n |
厚度 |
0.002 |
0.0004 |
0.0384 |
|
l |
叶片长 |
0.005 |
0.0004 |
0.0384 |
|
d |
双锥喉径 |
0.04 |
0.0004 |
3.214 |
|
D |
管径 |
0.05 |
0.00058 |
5.292 |
|
C |
流出系数 |
0.9651 |
0.00712 |
1 |
|
ε |
可膨胀系数 |
1 |
0.0032 |
1 |
|
ρ |
流体密度 |
996 |
0.0006 |
0.5 |
|
P |
差压 |
/ |
0.0045 |
0.5 |
|
|
|
|
|
|
系统不确定度由相对合成标准不确定度 u
cr(y)和差压传感器标准不确定度 u(s)组成,系统的合成标准不确定度为

|
2 |
|
|
ucr =姨ucr(y)+u2(s) =0.0083 |
(14) |
扩展不确定度:U
r =k·u
cr =0.0166,其中包含因子k=2。
通过对双锥流量计样机工作原理及测试数据的分析, 确定了其主要不确定度来源及不确定度值。 实验数据分析显示:样机合成标准不确定度为0.83%,扩展不确定度为 1.66%。
5、结语:
样机流量测试显示:在整个流量测量范围上小流量的测量误差波动较大,重复性表现也较差。 样机累积流量测量的***大误差在 0.6%以内,重复性在0.4%以内,流量计线性度在 1.5%以内。 通过对影响样机不确定度的因素分析发现:双锥流量计样机的流出系数 C、管道内径 D 对样机不确定度的影响较大; 可膨胀系数 ε、 双锥喉部与上游 1.5 D 的压差P、节流锥体喉部直径 d 影响次之;流体密度 ρ、叶片型固定架厚度 n 及长度 l 影响较小。 通过对双锥节流件特性及流量计测试的不断深入研究, 有助于双锥节流件及其流量计向标准化和产品化方向发展。

 导
导





