摘 要 以孔板流量计为例，比较孔板流量计的流量模型与流量积算仪中常用流量简化公式之间的差异。通过对孔径比、流出系数、可膨胀系数三个主要影响参数的分析，得出其可能引入的流量误差，并提出消除该流量误差的方法。

0 引言
 
差压式孔板流量计因价格低廉、维护成本低、
 
结构稳定等优点一直被广泛使用于流量计量装置中。但是由于其流量计算的复杂性，过去使用的流量二次仪表受限于仪表本身的计算能力，往往使用一些近似公式来简化流量的计算，不可避免会产生一定的误差。随着智能仪表的发展，可以用直接计算法代替过去的简化公式来计算流量，提高流量测量准确度。
 
1 孔板流量计流量计算模型
 
孔板流量计质量流量的流量计算模型 ^[1] 如式（1）所示。
 
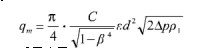
（1）
 
式中：q_m — 质量流量； C — 流出系数；
 
β — 直径比，β=d/D； D — 管道直径； ε — 可膨胀系数； d — 开孔直径；
 
p — 节流件前后取压口的差压； ρ₁ — 节流件正端取压口平面上的流体密度
 
其中可膨胀系数 ε 根据 GB/T 2624-2006 中给出的经验公式计算，如式（2）所示。

式中：p₁ — 节流件上游取压口平面上的静压； p₂ — 节流件下游取压口平面上的静压； κ — 等熵指数参照 GBT 2624.2-2006，流出系数 C 用 Reader-Harris/Gallagher(1998) 公式计算。
2 流量积算仪中的流量计算模型
 
在式（1）中，β 与 d 在不考虑孔板磨损和管道积污的情况下为常数；C 和 ε 的计算公式非常复杂，但在一定的流量范围内变化并不大，因此一般在流量积算仪中将 C 和 ε 看成常数 ^[3]，即式（1）在流量积算仪中被简化为式（3）。
 
 
3、流量误差分析：
 比较式（1）和式（3）可知，流量积算仪中使用的简化公式与流量理论值的误差主要来自于近似
的常数 K 与实际值之间的差别，分β、C、ε 三部分分别分析。
 
3.1、孔径比 ：
 通常孔板在制作过程中，孔板孔径加工误差限为 0.05%，由式（1）可知，加工误差引入到流量计


 

表 1	流量的***终影响量与 β 的取值关系
孔径比取值	< 0.45	0.50	0.55	0.60	0.65	0.70	0.75
0.05% 的孔径误差引入的流量相对误差	< 0.004%	0.007%	0.010%	0.015%	0.022%	0.032%	0.046%

  由 GB/T 2624.2-2006 中的流出系数公式可知，流出系数 C 是受孔板孔径比 β 和管道雷诺数 Re_D 影响的一个变量。而当孔板制作完成并经检验合格后，其孔径比 β 即为常数。此时，流出系数和雷诺数的关系可以用一条关系曲线来表示，以一 β 取 0.5 的典型孔板流量计为例，流出系数与雷诺数的关系曲线见图 1。



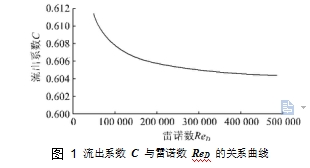
图 1 流出系数 C 与雷诺数 Re_D 的关系曲线

由图 1 可见，在雷诺数较小的区间内，雷诺数变化所引起的流量系数变化是非常可观的。以上图所取的典型孔板流量计为例，当取其量程比 1 ∶ 5 时，其雷诺数随流量变化的范围为 1×10⁵ 至 5×10⁵，而其流出系数变化范围为 0.608 至 0.604，即流出系数***大值与***小值存在 0.6% 以上的差别。因此若将流出系数取为固定值，流量积算仪中的流量计算值与实际值将会因流出系数的不同而引入不小的偏差。
 
3.3 可膨胀系数 ε

  在式（2）中，在 β 和等熵指数 κ 确定的情况下，可膨胀系数 ε 仅与节流件上游与下游取压口平面上的静压和有关。即流量变化引起差压变化，同时引起可膨胀系数 ε 的变化。
  同 3.2 中的例子，量程比取 1 ∶ 5，工况 取1.1 MPa 压力，***大差压为 80 kPa，此时***小差压为 3.2 kPa。可膨胀系数 ε 和流量的关系曲线见图 2。



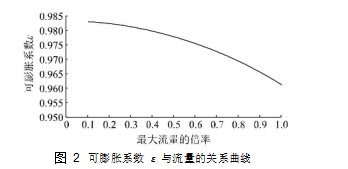
图 2 可膨胀系数 ε 与流量的关系曲线
  在满量程时可膨胀系数 ε 为 0.961 4，而在***小流量即满量程的 0.2 倍时，可膨胀系数 ε 为 0.982 3。可知在流量分别为***大和***小时，可膨胀系数 ε 相差 2% 以上，因此若将可膨胀系数简单设定为固定值会造成较大的流量误差。

4、解决方法：
 
 由前文分析可知，过去流量积算仪中常用的简化流量计算模型与理论计算模型之间存在着不小的误差，且由图 1 和图 2 可知，流出系数 C 和可膨胀系数 ε 都是随着流量的增大而减小，即将两者简化为常数会使两者的误差同向叠加造成更大的误差。
 随着智能二次仪表的发展，可以通过采用直接计算法代替简化计算公式来从根本上解决这一问题。例如孔径比 β 用实测值代替设计值、ε 用公式实时计算来代替固定值参与流量计算。需要特别注意的是，流出系数 C 需要使用迭代法来多次迭代才能求出其实际值。这是因为流出系数 C 是雷诺数 Re_D 的函数，而 Re_D 是质量流量 q_m 的函数，而 q_m 又是 C 的函数。因此在计算实际流出系数的过程中，首先需要设定一个初始流出系数 C₀，然后进行迭代计算，直到两次迭代结果之间的误差满足准确度要求，计算框图见图 3。
 
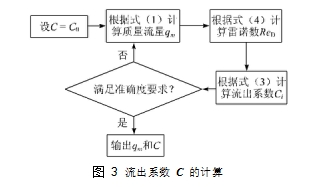
5、结语：
 本文以孔板流量计为例，比较了流量模型与流量积算仪中常用简化公式之间的差异，定量分析了其可能引入的误差，并给出了解决方法。虽然流量计的种类繁多，影响流量测量准确度的因素更多，但这种分析与解决的方法是具有普遍意义的。只要理清每个影响因素与流量之间的关系，通过功能越来越强大的智能仪表进行修正及计算，就可以得到更为准确的流量数据，提高流量测量准确度。