摘 要:叶轮是涡轮流量计的重要组成部分,根据理论模型可知,叶轮对涡轮流量计的计量性能具有一定的影响。 针对不同叶轮对涡轮流量计的影响,通过试验的方法,分析了改变叶轮倾斜角对涡轮流量计计量性能的影响。 结果表明,角度较大的叶轮 B 对其误差曲线影响较小;角度较小的叶轮 A 对其误差曲线影响较大。
涡轮流量计具有精度高、重复性好、结构简单、测量范围广、体积小、质量轻、压力损失小、维修方便等优点,被广泛应用在石油、化工、冶金、城市燃气管网等行业中
[1]。 随着涡轮流量计的大量使用,用户对其计量准确度的要求也越来越高。
叶轮倾斜角 θ 或叶片数 Z 是涡轮流量计设计中的重要参数,直接影响流量计的计量性能。 θ 角减小,当进入流量计被测流体流速相同时,叶轮速度将提高。 当其它条件不变时,随着 θ 角减小,叶轮转速增大,提高了仪表的灵敏度
[2]。 但转速提高使阻力矩增大,被测流体的压力损失增大,轴承磨损增大,仪表寿命降低。
在研发气体涡轮流量计的过程中, 针对叶轮倾斜角 θ 大小的改变对涡轮流量计性能的影响进行研究。
1、涡轮流量计的测量原理与结构:
1.1、基本结构:
涡轮流量计主要由整流器、叶轮、磁性联轴器、机械计数器、齿轮变速器等组件组成。
1.2、基本原理:
涡轮流量计是一种流体测量装置, 流体的动力驱使叶轮旋转,其旋转速度与体积流量近似成正比例。 通过流量计的流体体积是基于叶轮的旋转数得到的,主要是运用磁电转换装置或者机械输出装置将涡轮转速转化成电脉冲,送入二次仪表进行计算和显示,由单位时间内电脉冲和累计电脉冲数来反映瞬时和累计流量。
1.3、叶轮:
涡轮叶轮亦称叶轮,一般采用工程塑料、钢或铝合金材质,其作用是把流体动能转换成机械能。 按照设计要求,叶轮叶片数为 Z=12~20,叶片倾斜角 θ=30~45°,重叠度为 1~1.2,叶片与内机壳间隙为 0.5~1 mm。 为提高涡轮流量计的计量性能, 可适当增加叶片数或调整倾斜角
[3]。
1.4、理论依据:
涡轮流量计的数学模型为:
|
J |
dω |
|
=Tr-Trm-Trf-Tre |
|
|
(1) |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K= |
|
Z |
( |
tanθ |
- |
Trm |
- |
Trf |
) |
(2) |
|
|
|
|
22 |
22 |
|
|
|
2πrA |
|
r ρqv |
r ρqv |
|
|
q=f/K |
|
|
|
|
|
(3) |
式中:J 为涡轮的转动惯量;ω 为涡轮叶轮的旋转角速度;T
r 为流体对叶片产生的推动力矩;T
rm 为涡轮轴与轴承之间摩擦产生的机械摩擦阻力矩;T
rf 为流体通过涡轮时产生的流动阻力矩;T
re 为电磁转换器对涡轮产生的电磁阻力矩;Z 为涡轮叶片数;θ 为叶片倾斜角;r为叶片的平均半径;A 为流通截面积;ρ 为流体的密度; f 为信号脉冲频率;q 为体积流量;K 为仪表系数 ;q
v 为瞬时体积流量。
根据数学模型可以定性判断出涡轮流量计的计量性能与叶轮的叶片倾斜角有关, 笔者选取不同 θ 角的叶轮在同一台涡轮流量计上进行试验, 分析其对涡轮流量计的影响。
2、试验及试验数据分析:
2.1、试验介绍:
试验选取相同内径、外径的叶轮,只是叶轮的倾斜角、 叶片数及质量可能不 向沿顶圆展开同,对涡轮流量计的性能进行研究。 叶轮倾斜角的平面图如图 1 所示。
叶轮倾斜角平面图
2.2、试验及试验数据处理:
计算流量计的相对示▲图值误差为[4-6]:
|
Eij= |
Vij-(Vs)ij |
×100% |
|
|
|
|
|
|
(Vs)ij |
式中:E
ij 为第 i 检定点第 j 次检定被检流量计的相对示值误差,%;V
ij 为第 i 检定点第 j 次检定时流量计显示的累积流量值,m
3;(V
s)
ij 为第 i 检定点第 j 次检定时标准器换算到流量计处状态的累积流量值,m
3。
试 验 选 取 一 台 0.5 级 标 准 的 TGM/G250/DN80/ PN16 气体涡轮流量计, 选用两种不同参数的叶轮,在试验中研究叶轮对涡轮流量计计量性能的影响。试验所用叶轮 A 与 B 的差别见表 1。
|
|
表 1 |
叶轮对比 |
|
|
|
|
|
|
|
|
叶轮 |
角度 θ/(°) |
|
质量/g |
温度/℃ |
|
|
|
|
|
|
|
A |
35.5 |
|
38 |
20 |
|
|
|
|
|
|
|
B |
49 |
|
39 |
20 |
|
|
|
|
|
|
试验之前, 分别对装有不同叶轮的涡轮流量计进
|
行空载计时,见表 2。 |
|
|
|
|
|
表 2 |
自转时间s |
选用叶轮 A 时的试验 |
|
|
|
|
|
数据见表 3。 |
|
|
|
|
叶轮 |
|
自转时间 |
|
|
|
|
|
|
|
选用叶轮 |
|
时的试验 |
|
|
A |
|
142 |
B |
|
|
|
|
|
|
|
|
|
B |
|
160 |
数据见表 4。 |
|
|
|
|
|
|
|
|
|
|
|
根据表 3 和表 4 作出叶轮 A 和叶轮 B 的误差曲 |
线图,如图 2 和图 3 所示,叶轮 A 在流量 20~400 m
3/h时 ,0.5 级是合格的,在 100 m
3/h 误差出现突变情况;叶轮 B 在流量 12~400 m
3/h 时,0.5 级是合格的。
根据表 3 和表 4 作出叶轮 A 和叶轮 B 的误差对比图,如图 4 所示。由图 4 可以看出, 叶轮 B 的误差曲线在流量点50~400 m
3/h 的线性比叶轮 A 的线性要好; 在流量点8~12 m
3/h, 误差大概为-1%~-3%左右 , 均为不合格点。
3、结论:
通过试验, 分别对不同倾斜角叶轮进行研究,得出如下结论:
(1)叶轮 B 在小流量点的误差优于叶轮 A;
(2)两叶轮在流量点 100 m
3/h 都出现误差突变;
(3)叶轮 A 在线性区误差更趋近零点;
(4)叶轮 B 在线性区误差偏离零点 ,但是仍在误差范围内;
表 3 叶轮 A 试验数据
|
流量点/(m3·h-1) |
|
400 |
|
|
250 |
|
160 |
|
|
100 |
|
64 |
40 |
12.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
瞬时流量点/(m3·h-1) |
|
390.3 |
|
243.06 |
|
157.67 |
|
100.90 |
|
63.91 |
38.8 |
13 |
|
误差/% |
|
-0.4734 |
|
-0.270 8 |
-0.297 3 |
|
0.375 1 |
-0.355 1 |
-0.333 5 |
-3.034 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表 4 |
叶轮 B 试验数据 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
流量点/(m3·h-1) |
|
400 |
|
|
250 |
160 |
|
100 |
|
|
64 |
|
|
40 |
|
12.5 |
8 |
|
瞬时流量点/(m3·h-1) |
|
390.3 |
|
243.06 |
157.67 |
100.90 |
|
63.91 |
|
38.8 |
|
13 |
8.13 |
|
误差/% |
|
0.289 2 |
|
0.468 7 |
0.460 0 |
0.504 |
1 |
|
0.297 0 |
|
0.49 |
|
0.128 3 |
-3.243 1 |
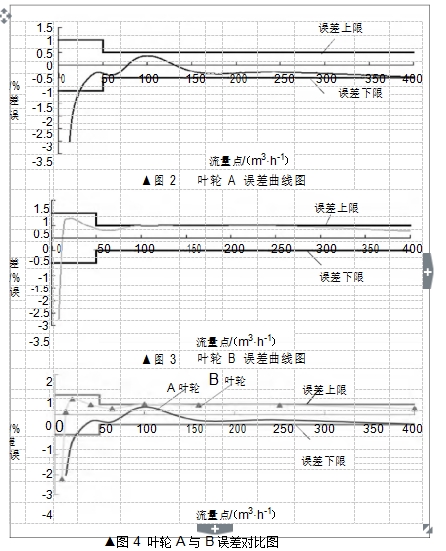
▲图 2
叶轮 A 误差曲线图
▲图 3
叶轮 B 误差曲线图
▲图 4 叶轮 A 与 B 误差对比图
(5)对于量程大的涡轮流量计,应该优选倾斜角较小的叶轮;而对于量程小的涡轮流量计,应该优选倾斜角较大的叶轮;
(6)在小流量点区域 ,不管是叶轮 A 还是叶轮 B,计量误差仍然很大。
总之, 叶轮倾斜角只影响误差曲线在线性区偏离零点的幅度,但是在小流量点误差仍然很大,给贸易计量带来了不公平,因此,接下来的研究工作主要是解决小流量点误差偏大的问题。

 导
导

