轮流量计是应用广泛的流量计量仪表。它的结构简单、灵敏度高、压力损失小。特别是其良好的重复性、稳定性倍受用户的青睐。但是长期以来，由于其非线性特性的存在，使其流量测量范围受到很大制约。通过对涡轮流量计输出脉冲信号特性的研究和分析，提出了一种扩大涡轮流量计量程范围的方法，这种方法简单易行、行之有效并可应用于其他脉冲频率输出的传感器中去。

1、涡轮流量传感器的工作原理：
  涡轮流量传感器结构如图 1 所示，属于速度式流量传感器。涡轮置于流体通道中，随着流体的流动产生旋转，设涡轮的转速为 n、流过涡轮的流体速度为 u，则 n 与 u 成正比; 流体通道的流通截面积 S 是已知的常数，所以，流过涡轮流量传感器的流体体积流量 Q 为:
Q = S × u

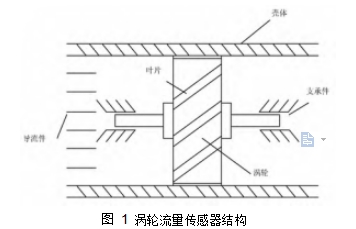
图 1 涡轮流量传感器结构

测量流体速度 u 通常是利用电磁感应原理将与流体速度成正比的涡轮转速 n 变成脉冲频率 F:
 

F = N × n

( 2)

 
  公式 ( 2) 中，N 是涡轮流量传感器的叶片数， n 是叶轮的旋转速度。涡轮流量传感器一旦选定，其叶片数 N 即为常数，所以信号频率 F 与转速 n 呈线性关系; 由于叶轮的转速 n 正比于流体的流速 u，对于截面积 S 恒定的流通管路，由公式 ( 1) 可见，流体速度 u 与流量 Q 之间也呈线性关系。所以，电脉冲信号频率 F 也就正比于流量 Q。在使用涡轮流量传感器时，只要测量出它的输出电脉冲信号频率F，就可以计算出相应的体积流量 Q。



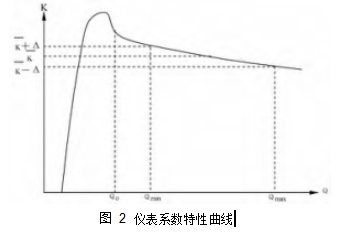
图 2 仪表系数特性曲线
虽然电脉冲信号频率 F 与体积流量 Q 是正比关系，但是其比值却不是常数。其原因是流体的摩擦阻力、粘滞阻力、磁电转换器的电磁阻力以及涡轮轴与轴承之间的机械摩擦阻力等都与流体的流动速F M度有关。可以用 K = _Q = _V 来表达各参数间的关系。
  式中，M 是涡轮传感器输出的电脉冲数，V 是流过涡轮传感器的流体体积，即 K 为通过单位流体流量涡轮流量传感器发出的电脉冲频率或单位体积流体涡轮流量传感器发出的电脉冲数，K 称为涡轮流量传感器的平均仪表系数。图 2 表示了 K 与 Q 之间的关系。以往常规使用方法是在涡轮流量传感器的测量范围 Q_min ～ Q_max 内，测得各流量检定点的仪表系数 K_i ，并将各 K_i 取平均值得到 K，把 K 作为该传感器的平均仪表系数。进行流量测量时，测得涡轮流量传感器发出的电脉冲频率 F，即可由 Q = ^F_K 得到相应的流量 Q 值，从而完成流量测量任务。

2 、涡轮流量传感器的测量范围：
  图 2 显示测量出电脉冲信号频率 F 用平均仪表系数 K 计算得到的 Q 值，在 Q_min ～ Q_max 范围内的***大相对误差为:

δmax	=	±			× 100%	( 3)
			K

 
 在 Q ＜ Q_min 或 Q ＞ Q_max ，即在测量范围之外误差将超过 δ_max 。这就是说虽然涡轮流量传感器具有很好的重复性，但是由于电脉冲信号频率 F 与体积流量 Q 之间是非线性的，按照常规的平均仪表系数 K 的计算方法，对于一定的误差限 ± ，由于非线性误差的存在使得涡轮流量传感器的工作范围只能限定在 Q_min ～ Q_max 之内。
 对于重复性很好而线性度较差的涡轮流量传感器，要扩大其测量范围或减小测量误差，研究的核心问题是设计一种便捷的使用方法，按照行鉴定规程利用原有检定数据，使涡轮流量传感器在具有很小重复性误差的流量范围内，都能得到很准确测量效果。
 
3、涡轮流量传感器的常规使用方法：
 像其它速度式流量计一样，涡轮流量传感器出厂时要按照涡轮流量传感器鉴定规程 ( JJG198 － 94) 的规定进行计量性能检定。传感器的量程比 α
^Qmax= _Qmin ^{一旦确定，其各流量检定点 Q}i ^{也就随即产}生^⑴ 。在量程范围即 Q_min ～ Q_max 内，规程规定了 n 个流量检定点。通过实流标定，得到相应检定点 Q_i ( i = 1 ～ n) 的仪表系数 K_i 。于是，平均仪表系数

K 为:

( Ki )

+

( Ki ) min

max

( 4)

K =

2

线性度 ( 非线性误差)

(

Ki )

－

( Ki ) min

( 5)

δ =

max

(

Ki )

max

+

( Ki ) min

按照公式 ( 5)  计算得到非线性误差 δ≤1． 0% ，

对于量程比 α = 10 的涡轮流量传感器，很难实现。

即采用平均仪表系数 K 计算流量的计量准确度达到

1． 0 级水平是一件很难是达到的指标;  而实际检定

数据显示，各流量检定点 Qi  上的仪表系数 Ki  的重

复性误差 Eri 基本都能达到 0． 1% 甚至 0． 01% 范围之

内。Eri 由公式 ( 6)  计算得到。

m

∑ ( Kij － Ki ) 2

( 6)

Eri =

j = 1

× 100%

( n － 1)  K2i

槡

式中:  Ki	=		1 ∑Kij ，m 是该流量检定点的检定
				m
			m j = 1

次数。
 
  涡轮流量传感器的重复性误差 E_r = E_rimax 通常情况下，涡轮流量传感器的量程比 α = 10、非线性误差 δ≥1． 0% 而重复性误差 E_r ≤0． 01。如果在使用涡轮流量传感器进行流量测量时不对仪表系数取平均值，即不用平均仪表系数 K，而是直接使用各流量检定点的检定仪表系数 K_i ，就有可能避免非线性误差对流量测量的影响。涡轮流量传感器的测量误差就有可能从线性度 δ = 1． 0% 变为重复性 E_ri = 0． 01% 。即涡轮流量传感器的制造工艺不变、遵循现行的计量检定规程、使用现有的检定数据，只是对检定数据的使用方法稍加改变就有可能成百倍地提高测量准确度。
 涡轮流量传感器输出的脉冲信号频率 F = N × n ( N 是涡轮叶片数，n 是涡轮的旋转速度) ; 流过涡轮流量传感器的被测流体体积流量 Q = S × u ( S 是流体的流通截面积，u 流体介质的流速) ; 涡轮流量
传感器在各检定点的仪表系数 Ki  = ^Fi ，并且各检定
Q_i
 
点的检定仪表系数 K_i 的重复性误差 E_ri y 远远小于其非线性误差 δ。在常规使用过程中，传感器得到的
流量 Qi  是通过 Qi  = ^Fi 的关系求得的。即流量计的
K_i
 
计算单元得到涡轮流量传感器输出的电脉冲频率 F，
通过 Q = ^F 计算出瞬时流量 Q。当 Q ＞ Q₀  之后，涡
K
 
轮流量传感器的仪表系数 K 与 Q 的关系近似线性的单调函数 ( 见图 2) 。因此，在对检定结果进行处理时，直接将各检定点的检定结果以 F_i 、K_i 的形式存入涡轮流量计的数值运算部分，不必对其仪表系数

取平均值。在使用涡轮流量传感器进行流量测量
时，根据涡轮流量传感器的信号频率 F，即可在以
上检定结果中检索各 Fi  值，找出满足 Fi ≤F≤Fi + 1
的 Fi 、Fi + 1  ( i = 1，2，…，n － 1) ，n 是该涡轮流量
传感器的流量检定点数;  若信号频率 F = Fi  或 F =
Fi + 1 ，则相应的 Ki  或 Ki + 1 即为所需的仪表系数;  若
信号频率 Fi ＜ F ＜ Fi + 1 ，即所测得的信号频率不正好
在检测频率点上，此时的仪表系数 K 可以用线性插
值公式 ( 7)			来计算:
K = Ki +		Ki + 1		－ Ki		( F － Fi )	( 7)
			Fi + 1
				－ Fi
	Ki		－ Ki + 1				( 8)
δmax =			+ Ki + 1
	Ki
这种计算方法的设计思路是在检定频率点上直
接用检定点的检定仪表系数，其误差就是该点的重

复性误差 δ_Ｒ ; 在检定频率点之间就采用相邻两个检定点的检定仪表系数 K_i 、K i + 1 的线性差值得到该点的仪表系数 K，由此带来的***大测量误差的极限值为 K_i 、K_{i + 1} 之间的非线性误差 δ'_max 。因为各计量检定点是按照鉴定规程 ( JJG198 － 94 ) 确定的，所以各检定点的非线性误差 δ'_max 与全量程非线性误差δ 之间应满足 δ'_max ≈ ^δ_n 。也就是说使用这种计算方法得到的测量结果其误差值只有采用平均仪表1系数时 _n ; 由于涡轮流量传感器的仪表系数 K 与流量 Q 之间当 Q≥Q₀ 时基本呈线性关系，所以用线性插值法得到的实际的测量误差 δ'_max 更接近重复性误差 E_Ｒ 而远小于非线性误差 δ'_max ，即 δ' ≈ E_Ｒ ＜
＜ δ'_max 。
 
  这种计算方法与平均仪表系数方法的区别在于涡轮流量计的数据存储区中存放的是 n 组实际检定结果而不是一个平均仪表系数 K; 使用流量计进行流量测量时，根据测得的频率值 F 找到与之相邻的一对检定频率点 ( F_i ，F_{i + 1} ) 及对应的一对检定仪表系数 ( K_i ，K_{i + 1} ) ，不是简单地用测得的频率值 F除以平均仪表系数 K 就得到了当前流量值; 根据 ( F_i ，F_{i + 1} ) 、( K_i ，K i + 1) ，先用公式 ( 7) 计算出对应信号频率 F 的仪表系数 K，然后用该频率值 F除以计算得到的仪表系数 K 得到当前流量 Q。这种方法可称之为 “检定系数折线法”。这种使用方法看似比用平均仪表系数繁琐，但在目前广泛采用的微机化仪表中非常容易实现; 采用此法在可编程控制器 ( PLC) 以及计算机检测、控制系统中进行流量测量，可以在确定的量程范围内提高涡轮流量传感器的测量精度或者在确保测量的前提下扩大测量范围。
 
4、实验数据分析: 
  被检仪表: 公称通径分别为 10mm 和 15mm 的涡轮流量传感器各一台; 检定装置: 静态称重法标准水流量检定装置，系统精度 ± 0． 2%。分别采用常规的平均仪表系数法和检定系数折线法进行标定，并与作为标准的静态称重法的检定结果进行比对，结果见表 1、表 2。

			表 1	实验数据比较
仪表口径:  10mm;						测量介质:  水
			用称重法	检定系数折线		平均仪表系数
	检测点			法计算结果		法的计算结果
			测得的	计算	误差	平均	误差
			系数
				系数	( %)	系数	( %)
	0． 32	( m3 / h)	2057． 58	2056． 41 0． 0569 2052． 45 0． 2493
	0． 50	( m3 / h)	2052． 02	2052． 30 0． 0136 2052． 45 0． 0210
	0． 70	( m3 / h)	2050． 04	2050． 01 0． 0015 2052． 45 0． 1176
	0． 80	( m3 / h)	2050． 58	2050． 25 0． 0161 2052． 45 0． 0912
	1． 00	( m3 / h)	2048． 36	2048． 70 0． 0166 2052． 45 0． 1997
	1． 10	( m3 / h)	2047． 47	2047． 62 0． 0073 2052． 45 0． 2432
			表 2	实验数据比较
仪表口径:  15mm;						测量介质:  水
			用称重法	检定系数折线		平均仪表系数
	检测点			法计算结果		法的计算结果
			测得的	计算	误差	平均	误差
			系数
				系数	( %)	系数	( %)
	1． 00	( m3 / h)	749． 32	749． 38	0． 0080 744． 187 0． 6850
	1． 55	( m3 / h)	745． 83	746． 41	0． 0778 744． 187 0． 2203
	2． 50	( m3 / h)	742． 25	742． 89	0． 0862 744． 187 0． 2610
	3． 00	( m3 / h)	740． 57	741． 73	0． 1566 744． 187 0． 4884
	4． 00	( m3 / h)	739． 35	739． 58	0． 0311 744． 187 0． 6542
	4． 50	( m3 / h)	738． 54	738． 59	0． 0068 744． 187 0． 7646

 
  从表 1 可见，在相同的量程范围 ( 0． 32m³ / h ～1． 10 m³ / h) 内，使用常规平均仪表系数法的***大非线性误差为 0． 2493%，而使用检定系数折线法的***大误差只有 0． 0569% ，误差减少了 4 倍多; 表 2 显示，使用常规平均仪表系数法的***大非线性误差为0． 7646%，在相同的量程范围 ( 0． 5m³ / h ～ 5． 0 m³ / h) 内，检定系数折线法的***大误差只有 0． 1566%，减少了近 5 倍。显然，在同样的测量准确度水平 ( 如对 10mm 涡轮取 0． 2 级、对 15mm 涡轮取 0． 5级) 下，采用检定系数修正法涡轮流量传感器的测量范围比使用常规的平均仪表系数法有了明显的扩大。